Sfard (1991), Wiskundige concepten als proces en object

Een internationaal perspectief op reken- en wiskundeonderwijs Nr. 1

Koeno Gravemeijer en Frans van Galen, Werkgroep Wiskunde voor Morgen

In een veelgeciteerd artikel trekt Anna Sfard (1991) een parallel tussen wat in de geschiedenis van de wiskunde heeft plaatsgevonden, en wat plaatsvindt tijdens het leren van wiskunde. Met een aantal voorbeelden laat ze zien dat wat eerst een proces is – een wiskundige procedure – op een gegeven moment in het denken een object wordt. Het onderscheid tussen proces en object kunnen we kort illustreren met het volgende voorbeeld: tellen is een proces – je telt bijvoorbeeld een aantal blokjes en stelt dan vast dat het er 8 zijn – maar je kunt ook redeneren over 8 als een op zichzelf staand getal: 8 is 2 minder dan 10, twee keer acht is 16 enzovoort. In dat laatste getal redeneren we over het getal 8 zoals we ook over concrete objecten redeneren; 8 fungeert als object. Dit onderscheid tussen proces en object is verhelderend voor het begrijpen van de geschiedenis van de wiskunde, maar helpt ons ook te begrijpen waarom wiskunde voor veel mensen zo lastig is.

In deze bijdrage illustreren we dit onderscheid tussen proces en object met voorbeelden van Sfard (1991). We trekken vervolgens een aantal conclusies die belangrijk zijn voor het onderwijzen van wiskunde:

• De eerste conclusie is dat de overgang van proces naar object lastig is en veel tijd kost.
• Een tweede conclusie is dat we er voortdurend op bedacht moeten zijn dat wat voor een leraar al een ‘wiskundig object’ is, voor de leerling een heel ander karakter kan hebben. Zonder dat besef is de kans groot dat leraar en leerling langs elkaar heen praten.
• Een derde conclusie is dat het bij leren van wiskunde uiteindelijk niet gaat om het kunnen maken van bepaalde opgaven, maar om het ontwikkelen van wiskundige denkobjecten.

We vatten in dit artikel ‘wiskundig’ ruim op, We volgen daarbij Sfard die het woord ‘mathematics’ ook gebruikt, wanneer wij zouden spreken van ‘rekenen’ of ‘rekenen-wiskunde’. In het artikel gaan we er steeds van uit dat ‘wiskunde’ ook het ‘rekenen’ omvat.

Het ontstaan van getallen

Anna Sfard (1991) analyseerde de geschiedenis van de wiskunde en vond een patroon van cycli, waarin processen werden omgevormd tot objecten, die weer onderwerp van nieuwe processen werden. Als voorbeeld beschrijft ze hoe getallen zich ontwikkelden.

In de geschiedenis van de wiskunde kwamen de natuurlijke getallen als eerste naar voren. Het proces van het tellen van concrete zaken leidde tot de vorming van natuurlijke getallen als objecten. Die natuurlijke getallen vormden de basis voor, onder meer, processen als delen en vermenigvuldigen.

Daarna leidde het proces van het delen van natuurlijke getallen tot de vorming van breuken als objecten. De ontstaansgeschiedenis van breuken als objecten is nog te zien in de notatie. Zo is ¾ in feite een verkorte notatie voor ‘3 gedeeld door 4’. Anders gezegd, ¾ verwijst naar het proces van het delen en is een aanduiding geworden voor de uitkomst van deze deling. Na verloop van tijd is men hiermee gaan redeneren zonder steeds aan delen te denken. De breuk ¾ heeft de status van een getal gekregen omdat men, net als bij de natuurlijke getallen, allerlei getalrelaties leerde kennen – zoals ¾ = 3 x ¼,  ¾ = ½ + ¼,  ¾ = 1 – ¼ en 2 x ¾ = 1 ½. 

Op een vergelijkbare manier kwamen ook de irrationale getallen tot stand via worteltrekken. Hier kregen notaties met een wortelteken, zoals √7, ook de status van getallen. Daarna volgden de negatieve getallen (via aftrekken) en de complexe getallen (via worteltrekken toegepast op negatieve getallen). De historische ontwikkeling wordt weergegeven in figuur 1. Steeds zien we dat wat eerst alleen maar de uitkomst van een wiskundig proces was, na verloop van tijd, werd opgevat als een object. 

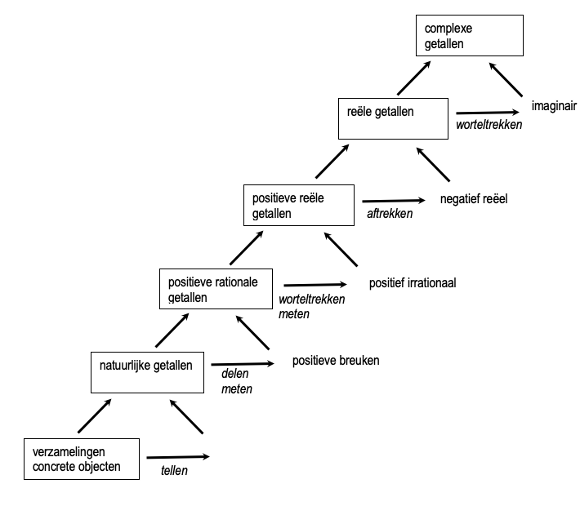
Deze ontwikkelingen hebben steeds heel wat voeten in de aarde gehad. En, zo betoogt Sfard, wat in het verleden lastig was voor wiskundigen, zal ook lastig zijn voor leerlingen.

Wiskundige objecten ontstaan door ervaring met, en reflectie op, wiskundige procedures en door die wiskundige procedures te comprimeren en te generaliseren en door symbolen en notaties te introduceren. Het kunnen redeneren in termen van wiskundige objecten biedt grote voordelen. Ze stellen ons in staat om een wiskundig concept in één oogopslag te herkennen en om er mee te werken zonder dat we ons in details hoeven te verdiepen. Dit speelt al bij de vorming van natuurlijke getallen.

Het ontstaan van functies als object

Proces-object overgangen vonden niet alleen bij de getallen plaats. Sfard(1991) zag bij allerlei wiskundige concepten een vergelijkbare ontwikkeling. Een voorbeeld is het wiskundige begrip functie. In de geschiedenis kwamen functies eerst naar voren als rekenvoorschriften die processen voorschrijven. De expressie f(x) = 2x + 3 wordt dan gezien als de opdracht om een inputgetal eerst met 2 te vermenigvuldigen en er vervolgens 3 bij op te tellen. Voor x = 4 wordt dat ‘2 × 4 = 8’, ‘8 + 3 =11’. Geleidelijk aan worden complexere functies echter verkort tot meer hanteerbare eenheden. Deelberekeningen worden daarbij deels uitgevoerd met behulp van symbolische representaties. Dat betekent dat functies kunnen worden geanalyseerd zonder ze uit te voeren. Van daaruit ontstaat het besef dat het inputgetal en het outputgetal kunnen worden gezien als samenhangende variabelen en daarmee verschuift da aandacht van individuele gevallen naar het geheel van alle mogelijke inputgetallen ‘x’ en de bijbehorende outputgetallen ‘f(x)’. De functie krijgt zo het karakter van een object. De grafiek van de functie biedt een krachtige ondersteuning van dit objectkarakter, de verzameling van input- en outputgetallen wordt als een geheel afgebeeld (figuur 2).

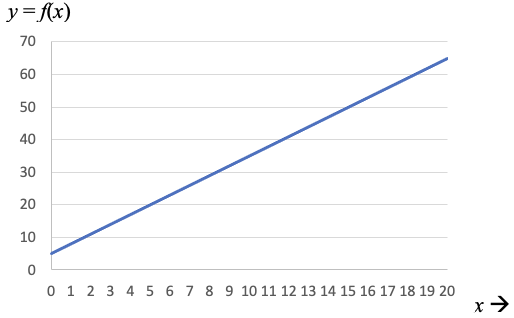
Dit leidde tot een nieuwe wiskundige definitie van een functie als een verzameling van geordende getallenparen (waarbij elk paar bestaat uit een inputgetal en een outputgetal).

Bij functies als objecten past ook het onderscheiden van kenmerken. Zo is f(x) = 2x + 3 een lineaire functie die zich onderscheidt van functies die een ander karakter hebben, zoals kwadratische en periodieke functies. Grafieken spelen hier weer een ondersteunende rol (figuur 3).

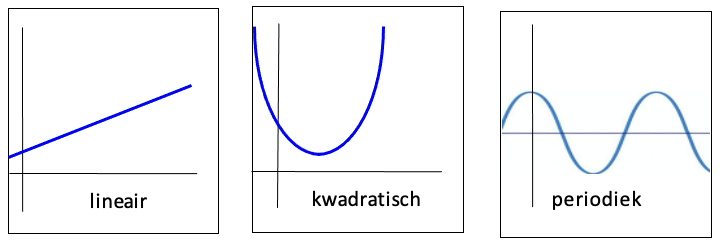
Sfard benadrukt dat de proces-object overgang niet absoluut is. Dit is waarom zij spreekt van de ‘dual nature’ van wiskundige concepten, proces en object zijn twee kanten van dezelfde medaille. De proceskant noemt zij ‘operational’, de objectkant, ‘structural’. Bij het oplossen van wiskundige problemen kan het heel handig zijn om het ene moment de objectkant te gebruiken en op het andere moment terug te gaan naar de proceskant.

Een bekend voorbeeld is dat van Wenger (1987).
Los v op uit: v√u = 1 + 2v√(1 + u).

Leerlingen die proberen de wortels kwijt te raken door kwadrateren lopen hopeloos vast. Leerlingen die √u en √(1 + u) als objecten zien, beseffen dat de structuur van de vergelijking neerkomt op: v ‘keer iets’ = 1 + 2v ‘keer nog iets’. Wat ‘iets’ en ‘nog iets’ zijn maakt weinig uit voor de manier waarop je de vergelijking oplost. Dit kan op een procedurele manier:

De onbekende naar één kant halen:               v√u − 2v√(1 + u) = 1
v isoleren:                                                        v (√u – 2√(1 + u)) = 1
Beide kanten door √ u – 2√(1 + u) delen:     v = 1/(√ u + 2 v√(1 + u)).

Sfard wijst er verder op dat niet alleen de processen die de basis voor de objecten leggen een belangrijke rol spelen, maar ook de processen waar de nieuwe objecten onderdeel van zullen worden. Het blijkt dat objectvorming wordt gestimuleerd door vooruit te lopen op de laatste soort processen. Zo kan er bij functies al worden gesproken over kenmerken als lineair en kwadratisch vóórdat de functies echt een object zijn geworden. Grafieken kunnen verder worden gebruikt om te onderzoeken wat het effect is van het veranderen van parameters. Of om te bepalen wanneer twee grafieken elkaar snijden. Mede dankzij de grafische representatie kan de functie in een vroeg stadium al als een geheel worden opgevat. Kortom, zowel het proces dat object wordt, als het proces waarin het object wordt gebruikt zijn essentieel voor de vorming van wiskundige objecten.

Conclusies

Wiskundige concepten hebben een proces- en een objectkant. De geschiedenis van de wiskunde laat een patroon zien van wiskundige processen die worden omgevormd tot objecten, die zelf weer onderwerp van nieuwe processen worden. Dit patroon zien we ook terug in het leren van wiskunde. Dit betreft niet alleen complexe begrippen als wiskundige functies maar ook simpeler zaken zoals de natuurlijke getallen. Een gedetailleerde beschrijving van hoe getallen-als-objecten ontstaan uit telprocessen is te vinden bij Gray en Tall (1994) (zie ook Een internationaal perspectief #1)

Als je kunt redeneren in termen van wiskundige objecten maakt dit de wiskunde een stuk eenvoudiger. Wiskundige objecten zijn op te vatten als gecomprimeerde processen, die verbonden zijn met specifieke notaties en met een netwerk van andere objecten en bredere verbanden. Dit betekent dat ze snel kunnen worden herkend, gemakkelijk te manipuleren zijn en dat de onderliggende processen onmiddellijk kunnen worden opgeroepen. Dit laatste is mede te danken aan het feit dat de verbinding met de oorspronkelijke processen bij objectvorming behouden blijft. Sfard spreekt in dit verband van een duaal karakter van wiskundige concepten. Terwijl Gray en Tall een samentrekking van de woorden proces en object tot het woord ‘procept’ gebruiken om dit duale karakter te benadrukken. De compacte, herkenbare, objecten die met een uitgebreid kennisnetwerk zijn verbonden, zorgen bovendien voor minder belasting van het werkgeheugen.

Wanneer concepten alleen gezien worden als procedures maakt dat wiskunde op een gegeven moment heel complex. Zo verwijst Sfard naar de tijd dat zelfs de meest complexe rekenprocessen werden beschreven met behulp van uitgebreide talige verhandelingen. Dat leidde tot een eeuwenlange stagnatie. Er kwam pas een doorbraak toen letters werden ingevoerd om berekeningen beknopt te beschrijven.

Wiskundige objecten zijn echter niet in kant-en-klare vorm over te dragen. Wanneer de leraar iets zegt over wiskundige objecten die de leerlingen nog niet als zodanig kennen, denken de leerlingen dat het over de processen gaat. Leraar en leerlingen praten dan langs elkaar heen. Een leraar die het, bijvoorbeeld, over een kwadratische functie heeft, denkt daarbij aan allerlei eigenschappen, zoals, symmetrie, 0, 1, of 2 nulpunten, één minimum of maximum, enz. Terwijl de leerlingen denken aan een functievoorschrift waar x² in voorkomt.

Tegelijkertijd leert de geschiedenis ons dat de stap van proces naar object heel lastig is. We moeten er daarom rekening mee houden dat deze stap ook in het onderwijs veel tijd en moeite zal kosten. We hebben echter het voordeel dat we uit de geschiedenis kennen af kunnen leiden waar mogelijkheden liggen om objectvorming te bevorderen.

Tot slot willen we benadrukken dat de wiskundige processen even belangrijk zijn als de wiskundige objecten. Dit betreft allereerst de onderliggende  processen waarop de leerlingen moeten reflecteren en die ze moeten verkorten en generaliseren. Waarbij goed gekozen representaties, symbolen en notaties belangrijke hulpmiddelen zijn. Maar ook de processen waarin met de objecten-in-wording wordt gewerkt spelen een belangrijke rol. Die werken als katalysator voor objectvorming.

Literatuur

Sfard, A. (1991). On the dual nature of mathematical conceptions: Reflections on processes and objects as different sides of the same coin. Educational studies in mathematics, 22(1), 1-36

Gray, E. M., & Tall, D. O. (1994). Duality, ambiguity, and flexibility: A ‘proceptual’ view of simple arithmetic. Journal for research in Mathematics Education, 25(2), 116-140.

Wenger, R. (1987). Cognitive science and algebra learning. In: A. H. Schoenfeld (eds.): Cognitive science and mathematics education, Lawrence Erlbaum Associates, London; 1987, p.p. 217-251.

Een overzicht van de verschillende manieren waarop wiskunde-didactici de vorming van wiskundige objecten beschrijven, is te vinden in:

Tall, D., Thomas, M., Davis, G., Gray, E., & Simpson, A. (1999). What is the object of the encapsulation of a process?. The Journal of Mathematical Behavior, 18(2), 223-241.